티스토리 뷰
sort 함수를 쓰면 끝나지만, 자료구조때 얼렁뚱땅 스킵했던 정렬에 대해 제대로 정리하고 직접 구현해볼 필요성을 느꼈다.
1. 선택 정렬
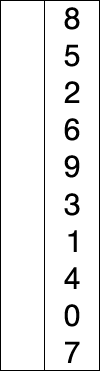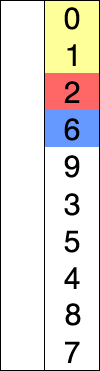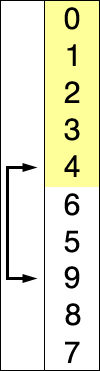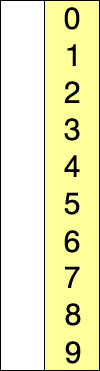
배열에서 가장 작은 데이터를 앞으로 보내는 정렬. (최댓값도 같이 처리한다던지의 개선 방법 존재)
1. 주어진 리스트 중 최소값 찾기(min)
2. 그 값을 맨 앞에 위치한 값과 교체(temp)
3. 해당 값을 제외한 나머지 리스트에서 반복
시간 복잡도

정렬해야하는 개수 N-1마다 (N-1, N-2, ... 1)번에 해당하는 비교 작업 + 교체 작업을 한다.
비교 시간복잡도
최악/최선에 상관없이 항상 같다.
N(N-1)/2 = O(n^2)
정렬 시간복잡도
3(N-1) = O(n)
공간 복잡도
배열 O(n), 교환용 상수 O(1)
소스 코드
#include <iostream>
using namespace std;
int main(int argc, char* argv[]) {
int num[8] = {9,1,6,8,4,3,2,0};
int minIndex(0), temp(0);
const int ARRSIZE = sizeof(num)/sizeof(int);
for(int i = 0; i < ARRSIZE; i++) {
for(int j = i; j < ARRSIZE; j++) {
if(j == i || num[j] < num[minIndex]) {
minIndex = j;
}
}
temp = num[i];
num[i] = num[minIndex];
num[minIndex] = temp;
}
return 0;
}2. 거품 정렬(버블 정렬)
인접한 원소의 크기를 검사하여 정렬을 반복
1. 리스트 index와 그 다음값의 크기 비교
2. 두 값이 역순이면 swap, 아니면 pass
3. 마지막 값을 제외한 리스트에 대해 다시 수행(가장 큰 값이 맨 뒤로 가기 때문.)

시간 복잡도

비교 시간복잡도
최상/평균/최악 모두 비교횟수는 같다.
1+2+ ... +n-1 = n(n-1)/2 = O(n^2)
이동 시간복잡도
최악(역순 정렬) : 비교 횟수마다 swap(3회)을 하니까 3n(n-1)/2 = O(n^2)
최선(이미 정렬됨) : 이동을 아예 안하므로 O(1)
평균 : O(n^2)
공간 복잡도
배열 O(n) 교환용 상수 O(1)
소스 코드
#include <iostream>
using namespace std;
int main(int argc, char* argv[]) {
int num[8] = {9,1,6,8,4,3,2,0};
int temp(0);
const int ARRSIZE = sizeof(num)/sizeof(int);
for(int i = 0; i < ARRSIZE; i++) {
for(int j = 0; j < ARRSIZE - i - 1; j++) {
if(num[j] > num[j+1]) {
temp = num[j];
num[j] = num[j+1];
num[j+1] = temp;
}
}
}
return 0;
}3. 삽입 정렬
정렬된 배열 부분과 주어진 요소를 비교해 내 위치를 찾아 삽입하는 정렬
1. 두번째 원소를 앞과 비교해 적절한 위치에 삽입한다.
2. 마지막 원소까지 반복한다.

시간 복잡도

비교 시간복잡도
최악(역순 정렬) : 모든 요소가 앞 정렬부분에 대해 모두 비교한다.
n-1+n-2+n-3+...2+1 = n(n-1)/2 = O(n^2)
최선(이미 정렬됨) : 모든 요소가 한번만 비교하고 끝난다.
n-1 = O(n)
이동 시간복잡도
최악(역순 정렬) : 모든 요소에 있어서, 앞 정렬부분이 계속 뒤로 밀리는 이동을 한다.
(n-1+n-2+...+2+1) = n(n-1)/2 = O(n^2)
최선(이미 정렬됨) : 이동을 아예 안하므로 O(1)
평균 : O(n^2)
공간 복잡도
배열 O(n) 교환용 상수 O(1)
소스 코드
#include <iostream>
using namespace std;
int main(int argc, char* argv[]) {
int num[8] = {9,1,6,8,4,3,2,0};
int temp(0);
const int ARRSIZE = sizeof(num)/sizeof(int);
for(int i = 1; i < ARRSIZE; i++) {
temp = num[i];
int j = i-1;
while(j >= 0 && num[j] > temp) {
num[j+1] = num[j];
j--;
}
num[j+1] = temp;
}
return 0;
}함수 안 쓴 버전
#include <iostream>
using namespace std;
void insert_sort(int list[], int first, int last, int gap = 1);
int main(int argc, char* argv[]) {
int num[11] = {10, 8, 6, 20, 4, 3, 22, 1, 0, 15, 16};
const int ARRSIZE = sizeof(num)/sizeof(int);
insert_sort(num,0,ARRSIZE);
return 0;
}
void insert_sort(int list[], int first, int last, int gap) {
int temp, j;
for(int i = first+gap; i <= last; i+=gap) {
temp = list[i];
for(j = i-gap; j >= first && list[j] > temp; j -= gap) {
list[j+gap] = list[j];
}
list[j+gap] = temp;
}
}함수 쓴 버전. 셸 정렬을 코딩하기 위해서 함수로 변경하고 gap도 추가한 모습이다.
gap의 default 값인 1에서는 기본 삽입 정렬과 동일하게 작동한다.
4. 셸 정렬
삽입 정렬은 어느정도 정렬된 리스트에서 굉장히 빠른 점(비교 및 이동이 유동적)에서 착안, 삽입 정렬을 보완한 방법.
전체 리스트를 일정 간격(gap)으로 나눠 부분 리스트마다 삽입 정렬하고 gap을 1이 될때까지 줄이면서 반복함.
1. 리스트를 일정 간격으로 나눈 후, gap 만큼 떨어진 요소들끼리 삽입 정렬 진행
2. 리스트를 더 촘촘하게 나눈 후, gap 만큼 떨어진 요소들끼리 삽입 정렬 진행
3. gap이 1이 될때까지 반복
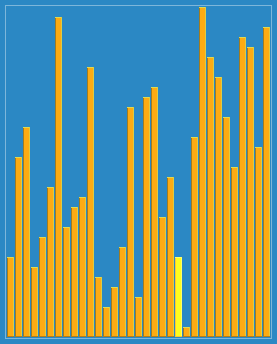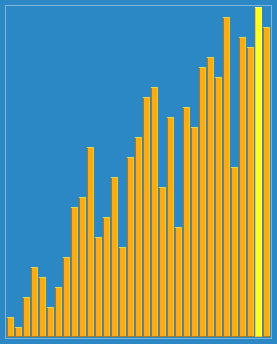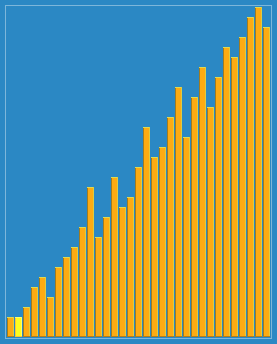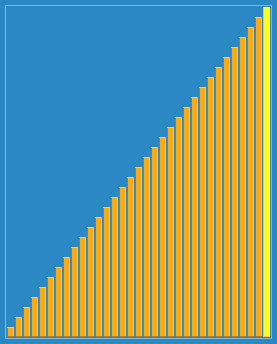
시간 복잡도
최악(역순 정렬) : 삽입 정렬과 비슷하게 된다.
n-1+n-2+n-3+...2+1 = n(n-1)/2 = O(n^2)
최선(이미 정렬됨) : O(nlogn)
각 gap에 대한 비교횟수는 1회가 되므로?
평균 : O(nlogn), O(n^1.25) 즈음이라고 한다.
왜인지는 모름. 평균은 삽입정렬보다 성능이 좋다.
gap을 어떻게 선택하느냐에 따라 시간복잡도에 변동이 존재한다고 한다.
공간 복잡도
배열 O(n) 교환용 상수 O(1)
소스 코드
#include <iostream>
using namespace std;
void insert_sort(int list[], int first, int last, int gap = 1);
void shell_sort(int list[], int size);
int main(int argc, char* argv[]) {
int num[11] = {10, 8, 6, 20, 4, 3, 22, 1, 0, 15, 16};
const int ARRSIZE = sizeof(num)/sizeof(int);
shell_sort(num, ARRSIZE);
return 0;
}
void insert_sort(int list[], int first, int last, int gap) {
int temp, j;
for(int i = first+gap; i <= last; i+=gap) {
temp = list[i];
for(j = i-gap; j >= first && list[j] > temp; j -= gap) {
list[j+gap] = list[j];
}
list[j+gap] = temp;
}
}
void shell_sort(int list[], int size) {
int gap;
bool isGapOne = false;
for(gap = size/2;isGapOne == false; gap = gap/3+1) { //gap 초기값은 /2, 이후 /3+1을 해서 gap이 1이 될때까지
if(gap == 1) {
isGapOne = true;
}
for(int i = 0; i < gap; i++) { //모든 부분리스트에 대해서
insert_sort(list, i, size, gap);
}
}
}좀 애먹음...ㅠㅠ
보면 gap이 항상 홀수이도록 하던데 그건 이해못해서 넣진 않았다. 그냥 조건문 하나 더해주면 끝이다.
5. 합병 정렬
리스트를 균등하게 분할하여 정렬한 후 다시 합침
1. 배열을 같은 크기의 2개의 부분 배열로 분할
2. 부분 배열의 크기가 충분히 작아질때까지 재귀 호출로 분할함
3. 충분히 작아진 부분 배열을 정렬
4. 정렬된 부분 배열을 하나의 배열로 통합
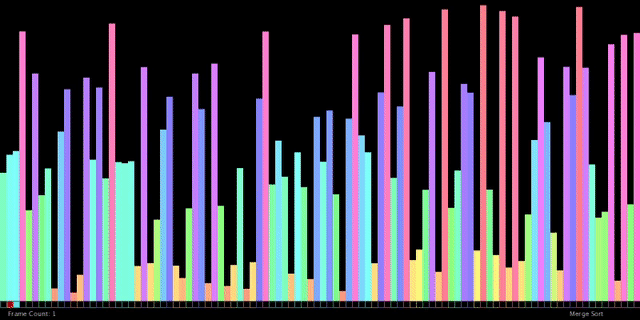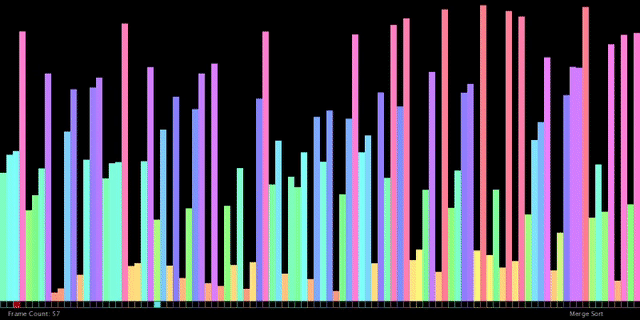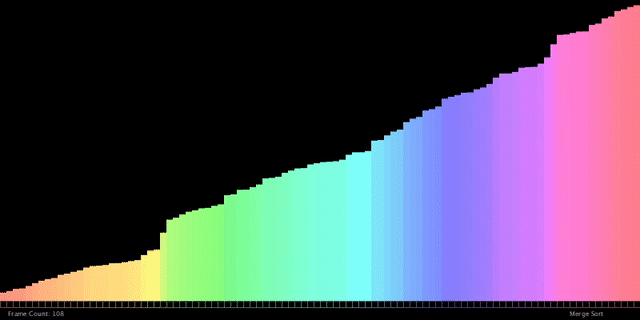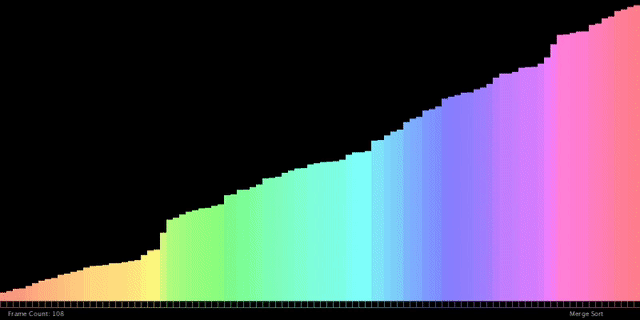
시간 복잡도
비교 시간복잡도
정렬 시간복잡도
공간 복잡도
소스 코드
'■ 알고리즘 > ◻ 개념' 카테고리의 다른 글
| 힙(Heap)에 대한 간략정리와 C++ 관련 라이브러리 및 함수 (0) | 2022.11.23 |
|---|---|
| 해시(Hash) 간단하게 정리 (0) | 2022.11.08 |
| C++ 기초 (0) | 2022.10.20 |
| 파이썬 재활 (0) | 2022.08.11 |
| C언어 기억 안났던것들 정리 (0) | 2021.09.06 |
