티스토리 뷰
요약
- 분할 정복을 위한 점화식 만들기
풀이과정
문제 풀이 방법은 금방 떠올린데 반해, 코드를 깔끔하게 다시 짜는데에 있어서 좀 많이 애먹었다.
시간도 오래 걸렸다.
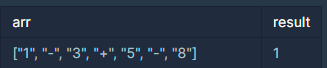
1. 숫자와 연산자 분리하기
이렇게 안해도 되는데 직관적인 코딩을 위해 분리하였다.
void init(vector<string> arr, vector<int> &nums, vector<string> &ops) {
// 숫자와 연산자로 나눠 저장
for(int i = 0; i < arr.size(); i++) {
if(i%2 == 0) {
nums.push_back(stoi(arr[i]));
}
else {
ops.push_back(arr[i]);
}
}
}2. 풀 방법 정하기
나는 Bottom-Top 방식의 문제풀이 방법을 택했다.
가장 작은 단위의 연산은 최대값이 명백하게 정해져있다.
이를 이용해 Top까지 올라간다.
숫자 크기의 2차원 배열을 2개 max_dp, min_dp로 선언한다. 하나는 max, 하나는 min값을 저장한다.
매번 max, min 을 통해 비교해줄것이기 때문에 초기화값은 아주 큰 음수와 양수로 한다.
이들 값의 중앙값은 무조건 숫자 본인이 된다.
이 예제의 경우
| 1 | |||
| 3 | |||
| 5 | |||
| 8 |
이 저장된다는 얘기다.
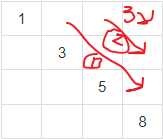
이 순서로 채워넣는 것을 반복할 수 있다.(이전 값을 쓰기 때문에.)
| 1 | -2 | ||
| 3 | 8 | ||
| 5 | 13 | ||
| 8 |
이렇게? 물론 저 단계까지는 max_dp, min_dp 모두 같기 때문에...
이후부터는 max와 min 값이 달라지게 된다.
여기서 기존 배열을 채우는 방법이 아니라, 대각선으로 내려가는 방식으로 채워야 하기 때문에 코드를 참 더럽게 짰었다.
https://school.programmers.co.kr/questions/35224
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
그런데 이 분의 설명에서 답을 찾았다.
step이라는 변수를 추가하는 것...!
그냥 이분의 해설과 같은 풀이이므로 이 해설을 보는 게 나을 듯.
코드
#include <bits/stdc++.h>
using namespace std;
const int INF = 9e8;
void init(vector<string> arr, vector<int> &nums, vector<string> &ops) {
// 숫자와 연산자로 나눠 저장
for(int i = 0; i < arr.size(); i++) {
if(i%2 == 0) {
nums.push_back(stoi(arr[i]));
}
else {
ops.push_back(arr[i]);
}
}
}
int solution(vector<string> arr)
{
int answer = -1;
vector<int> nums;
vector<string> ops;
init(arr, nums, ops);
int max_dp[nums.size()][nums.size()];
int min_dp[nums.size()][nums.size()];
for(int step = 0; step < nums.size(); step++) {
for(int i = 0; i < nums.size() - step; i++) {
int j = i + step;
if(step == 0) {
max_dp[i][j] = nums[i];
min_dp[i][j] = nums[i];
} else {
max_dp[i][j] = -INF;
min_dp[i][j] = INF;
for(int k = i; k < j; k++) {
// dp(i,k) dp(k+1,j)
// 연산자 검사 ops[k]
if(ops[k] == "+") {
//max = max + max
max_dp[i][j] = max(max_dp[i][j], max_dp[i][k] + max_dp[k+1][j]);
//min = min + min
min_dp[i][j] = min(min_dp[i][j], min_dp[i][k] + min_dp[k+1][j]);
}
else {
//max = max - min
max_dp[i][j] = max(max_dp[i][j], max_dp[i][k] - min_dp[k+1][j]);
//min = min - max
min_dp[i][j] = min(min_dp[i][j], min_dp[i][k] - max_dp[k+1][j]);
}
}
}
}
}
// for(int i = 0; i < nums.size(); i++) {
// for(int j = 0; j < nums.size(); j++)
// cout << max_dp[i][j] << " ";
// cout << endl;
// }
answer = max_dp[0][nums.size()-1];
return answer;
}
다른 사람의 풀이
'■ 알고리즘 > ◻ Programmers' 카테고리의 다른 글
| [C++]디스크 컨트롤러 (0) | 2023.03.10 |
|---|---|
| [C++]등굣길 (0) | 2023.03.10 |
| [C++]전력망을 둘로 나누기 (0) | 2023.03.01 |
| [C++]주식 가격 (1) | 2023.01.06 |
| [C++] 다리를 지나는 트럭 (0) | 2023.01.05 |
