티스토리 뷰
요약
- 경우의 수 파악
풀이과정
솔직히 이렇게 풀라고 낸 의도는 아닐텐데...
수학식을 세워서 풀었다.
자릿수마다 A,E,I,O,U가 가능하니 5를 그만큼 곱한다.
A _ _ _ _ 의 경우의 수는
5자리인 경우 5*5*5*5
4자리인 경우 5*5*5
3자리인 경우 5*5
2자리인 경우 5
1자리인 경우 1(5^0)
인 것이다.
예를 들어,
맨 앞자리가 E이면 A _ _ _ _ 인 경우의 수만큼 앞에 존재하는 것이라 생각해서 식을 세웠다.
| AAAAE | A | (1-1)*(5^4+5^3+5^2+5^1) + 1 |
| A | (1-1)*(5^3+5^2+5^1) + 1 | |
| A | (1-1)*(5^2+5^1) + 1 | |
| A | (1-1)*(5^1) + 1 | |
| E | 2 |
| AAAE | A | (1-1)*(5^4+5^3+5^2+5^1) + 1 |
| A | (1-1)*(5^3+5^2+5^1) + 1 | |
| A | (1-1)*(5^2+5^1) + 1 | |
| E | (2-1)*(5^1) + 1 |
| I | I | (3-1)*(5^4+5^3+5^2+5^1) + 3 |
| EIO | E | (2-1)*(5^4+5^3+5^2+5^1) + 2 |
| I | (3-1)*(5^3+5^2+5^1) +3 | |
| O | (4-1)*(5^2+5^1) + 4 |
코드
#include<bits/stdc++.h>
using namespace std;
int ctoi(char c)
{
int num;
switch(c)
{
case 'A':
num = 1;
break;
case 'E':
num = 2;
break;
case 'I':
num = 3;
break;
case 'O':
num = 4;
break;
case 'U':
num = 5;
break;
}
return num;
}
int solution(string word) {
int answer = 0;
for(int i = 0; i < word.length(); i++)
{
int powSum = 0;
for(int j = 4-i; j>0; j--)
powSum += pow(5,j);
answer += (ctoi(word[i])-1) * powSum + ctoi(word[i]);
}
return answer;
}

다른 사람의 풀이
첫번째 풀이
같은 풀이 방식이나 더 간결하게 정리한 코드이다.
#include <string>
using namespace std;
int solution(string word) {
string v = string("AEIOU");
int a = word.size();
for(int i = 0, b = 1; i < word.size(); i++, b *= 5)
a += v.rfind(word[i]) * 781 / b;
return a;
}v.rfind(word[i])
"AEIOU"에서 word의 각 자리수와 일치하는 index를 반환한다.
내가 쓴 코드에서 ctoi switch문으로 장황하게 A:1 E:2 I:3 O:4 U:5 한것을 하나로 일축한 방식이다.
781
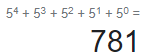
이 값이다.
예를들어, 위 예제 중 EIO에서 'I'는 (3-1)*(5^3+5^2+5^1) +3 라는 식을 도출했다.
3끼리 식을 묶으면
3(5^3+5^2+5^1+5^0)-(5^3+5^2+5^1)
식을 하나로 통합하려면
3(5^3+5^2+5^1+5^0)-(5^3+5^2+5^1+5^0)+5^0 = 2*(5^3+5^2+5^1+5^0)+1
이게 된다.
| EIO | E | (1)*(5^4+5^3+5^2+5^1+5^0) + 1 |
| I | (2)*(5^3+5^2+5^1+5^0) +1 | |
| O | (3)*(5^2+5^1+5^0) + 1 |
2에 해당하는 값은 'A':0, 'E':1, 'I':2, 'O':3, 'U':4 를 그대로 가져가면 된다.
매번 781을 b= 5, 5^2, 5^3 ... 이렇게 나눠준 이유는, 소숫점 자리 이하를 버리는 것이 Default이기 때문이다.
5^4+5^3+5^2+5^1+1 을 5로 나누면?
5^3+5^2+5^1+1+0.2 가 된다.
여기서 0.2는 버려진다.
따라서 깔끔하게, 5^3+5^2+5^1+1 이 되는 것.
맨 뒷 항의 +1 은 자릿수마다 생기므로 맨 앞에서 a = word.size(); 를 해준 이유가 된다.
1. rfind를 통해 index로 AEIOU를 01234로 바꿔먹은 것
2. 나머지가 안생기는 점을 이용해 5로 나누는 것
이건 기억해두면 좋을 것 같다.
위 코드를 기반으로 내 코드를 수정해봤다.
#include<bits/stdc++.h>
using namespace std;
int solution(string word) {
int answer = 0;
string s = "AEIOU";
int powSum = 0;
for(int i = 0; i < 5; i++)
powSum += pow(5,i);
for(int i = 0; i < word.length(); i++)
{
answer += s.rfind(word[i]) * powSum + 1;
powSum/=5;
}
return answer;
}781을 상수로 그대로 쓰는건 실제로는 좋지 않다 생각해서
외부에서 powSum으로 계산하는 과정을 추가했다.
첫 풀이는 어찌됐든간에 이중 반복문이라 O(n^2)의 시간복잡도를 지녔지만,
두번째 풀이에서는 O(n)이 되어서 시간이 확실히 줄었다.
두번째 풀이
그냥 거듭제곱의 합 계산에서 DP를 쓰는 방법이다. DP[0] = 1, DP[1] = 5를 주고
DP[2]부터 DP[5] 까지 DP[i] = 5*(DP[i-1]+1)으로 구하는 방법이다. 그 외는 같다.
'■ 알고리즘 > ◻ Programmers' 카테고리의 다른 글
| [C++]입국심사 (0) | 2023.05.03 |
|---|---|
| [C++]단속카메라 (0) | 2023.04.28 |
| [C++] 아이템 줍기 (0) | 2023.03.13 |
| [C++]단어 변환 (0) | 2023.03.13 |
| [C++]이중우선순위큐 (0) | 2023.03.10 |
